В этой статье мы спроектируем и напишем красивый, структурированный класс квадратного уравнения. Это уравнение вида a*x^2 + b*x + c = 0. Класс сможет находить корни уравнения. Он будет соответствовать парадигме ООП.
Поля и конструкторы
Класс назовём QuadraticEquation. Такое содержательное название лучше всего отражает его суть. Что должно хранить в себе квадратное уравнение, выстроенное согласно объектно-ориентированной парадигме? Логично, что это его коэффициенты: a, b и c. Они однозначно характеризуют разные уравнения этого типа. Так что добавим три приватных поля типа double. Впоследствии эти скрытые от глаз внешних наблюдателей данные будут использоваться в методах класса.
|
1 2 3 4 5 6 7 8 9 10 11 |
/** * класс, представляющий собой квадратное уравнение * с коэффициентами a, b, c * * @version 1.0, 01.12.2023 */ public class QuadraticEquation { private double a; private double b; private double c; } |
Отлично. Чтобы задать значения коэффициентов сразу при создании объекта QuadraticEquation, создадим конструктор. В нём будет три параметра типа double, которые будут соответствовать этим трём коэффициентам квадратного уравнения.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
/** * класс, представляющий собой квадратное уравнение * с коэффициентами a, b, c * * @version 1.0, 01.12.2023 */ public class QuadraticEquation { private double a; private double b; private double c; /** * конструктор с заданием всех коэффициентов сразу */ public QuadraticEquation(double a, double b, double c) { this.a = a; this.b = b; this.c = c; } } |
Этого может быть вполне достаточно для управления коэффициентами a, b и c. Однако давайте предоставим возможность также менять коэффициенты после создания объекта. Это можно сделать при помощи сеттеров и второго конструктора без аргументов. Он будет выставлять значения коэффициентам по умолчанию (нули). Помимо прочего, добавим геттеры, чтобы извне можно было получить значения коэффициентов. Если для решаемой задачи это не нужно, их можно не прописывать. Но в качестве примера добавим.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
/** * класс, представляющий собой квадратное уравнение * с коэффициентами a, b, c * * @version 1.0, 01.12.2023 */ public class QuadraticEquation { private double a; private double b; private double c; /** * конструктор с заданием всех коэффициентов сразу */ public QuadraticEquation(double a, double b, double c) { this.a = a; this.b = b; this.c = c; } /** * конструктор без аргументов * с начальными значениями коэффициентов - нулями, * чтобы коэффициенты можно было изменить позже */ public QuadraticEquation() { a = 0; b = 0; c = 0; } public double getA() { return a; } public void setA(double a) { this.a = a; } public double getB() { return b; } public void setB(double b) { this.b = b; } public double getC() { return c; } public void setC(double c) { this.c = c; } } |
Чудно, подготовительный этап завершён. Приступим к математической части!
Нахождение корней
Чтобы наш класс был более-менее полезным, нужно научить его решать себя. То есть находить корни своего квадратного уравнения. Согласно хорошему тону и идее чистого кода, каждый метод должен решать только одну задачу. Тогда метод будет чистым. Когда удаётся разбить сложную задачу на маленькие – работа значительно упрощается.
В рамках квадратных уравнений одна из таких маленьких задач – вычисление дискриминанта. И хотя это вычисление происходит в одну строку, хорошим тоном будет выделить его в отдельный метод. По названию метода calcDiscriminant() можно сразу понять, что вычисляется. По формуле Math.pow(b, 2) – 4 * a * c – придётся задуматься. А это затраты времени и сил.
|
1 2 3 4 5 6 |
/** * расчёт дискриминанта квадратного уравнения */ private double calcDiscriminant() { return Math.pow(b, 2) - 4 * a * c; } |
Теперь давайте продумаем все варианты решения. В квадратном уравнении может быть несколько ситуаций:
- дискриминант < 0, тогда корней нет,
- дискриминант == 0, тогда корень один,
- дискриминант > 0, тогда корней два,
- и два варианта, когда a == 0:
- b != 0, тогда корень один (x = -c/b),
- b == 0, тогда корней бесконечное множество.
Для всех этих ситуаций я предлагаю создать отдельные методы. Тогда в общем методе нахождения корней будет легко проследить логику их вызовов. Напишем методы для каждого из этих вариантов. Во всех случаях набор корней будем возвращать как массив double, так как количество корней заранее неизвестно.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
/** * получить отсутствие корней (0 корней), * пустой массив */ private double[] getNoRoots() { return new double[0]; } /** * рассчитать единственный корень * (когда дискриминант = 0) */ private double[] calcOneRoot() { double root = (-b) / (2 * a); double[] roots = { root }; return roots; } /** * рассчитать два корня уравнения * исходя из дискриминанта */ private double[] calcTwoRoots(double discriminant) { double rootOfDiscriminant = Math.sqrt(discriminant); double firstRoot = (-b + rootOfDiscriminant) / (2 * a); double secondRoot = (-b - rootOfDiscriminant) / (2 * a); double[] roots = { firstRoot, secondRoot }; return roots; } /** * рассчитать корень линейного уравнения, * то есть когда a = 0 и остаётся уравнение вида bx + c = 0, * которое легко решается переносом коэффициента c на правую часть с минусом * и делением его на коэффициент b */ private double[] calcRootOfLinearEquation() throws QuadraticEquationException { if (b == 0) { throw new QuadraticEquationException("Корней бесконечное множество"); } double root = -c / b; double[] roots = { root }; return roots; } /** * расчёт дискриминанта квадратного уравнения */ private double calcDiscriminant() { return Math.pow(b, 2) - 4 * a * c; } |
Как видите, я решила обработать случай, когда корней бесконечное множество, выбросом исключения. Ну не будем же мы возвращать бесконечность элементов double? А вернуть пустое множество корней будет обманом. Ведь корни-то есть, просто их бесконечно много. Бросать исключение в исключительных ситуациях это хорошая манера. Так мы даём понять тому, кто будет извне вызывать метод нахождения корней, что случилось что-то, выходящее за рамки ожидаемого.
Класс исключения QuadraticEquationException выглядит самым обычным образом, наследуясь от базового класса исключений Exception:
|
1 2 3 4 5 |
public class QuadraticEquationException extends Exception { public QuadraticEquationException(String message) { super(message); } } |
Супер. Осталось объединить логику написанных маленьких частей решения уравнения в один общий публичный метод, который и будет вызываться извне. Назовём его findRoots().
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
/** * нахождение всех корней квадратного уравнения, * причём их число может быть разным - от 0 до 2-х */ public double[] findRoots() throws QuadraticEquationException { if (a == 0) { return calcRootOfLinearEquation(); } double discriminant = calcDiscriminant(); if (discriminant < 0) { return getNoRoots(); } else if (discriminant == 0) { return calcOneRoot(); } else { return calcTwoRoots(discriminant); } } /** * получить отсутствие корней (0 корней), * пустой массив */ private double[] getNoRoots() { return new double[0]; } /** * рассчитать единственный корень * (когда дискриминант = 0) */ private double[] calcOneRoot() { double root = (-b) / (2 * a); double[] roots = { root }; return roots; } /** * рассчитать два корня уравнения * исходя из дискриминанта */ private double[] calcTwoRoots(double discriminant) { double rootOfDiscriminant = Math.sqrt(discriminant); double firstRoot = (-b + rootOfDiscriminant) / (2 * a); double secondRoot = (-b - rootOfDiscriminant) / (2 * a); double[] roots = { firstRoot, secondRoot }; return roots; } /** * рассчитать корень линейного уравнения, * то есть когда a = 0 и остаётся уравнение вида bx + c = 0, * которое легко решается переносом коэффициента c на правую часть с минусом * и делением его на коэффициент b */ private double[] calcRootOfLinearEquation() throws QuadraticEquationException { if (b == 0) { throw new QuadraticEquationException("Корней бесконечное множество"); } double root = -c / b; double[] roots = { root }; return roots; } /** * расчёт дискриминанта квадратного уравнения */ private double calcDiscriminant() { return Math.pow(b, 2) - 4 * a * c; } |
Да, методу findRoots() также пришлось обозначить в его шапке, что он может выбросить QuadraticEquationException. Что ж, поздравляю – наш класс научился математике. Однако есть ещё одна нужная часть. Это – как мы эти данные пользователю отдадим.
Категорически не рекомендуется писать такие методы, где одновременно происходит и расчёт корней, и, скажем, вывод в консоль. Во-первых, вы нарушаете логику приложения, заставляя один метод как рабочую лошадку и рассчитывать, и выводить. Это целых две задачи, и необходимо их разграничивать. Во-вторых, мы с вами не знаем, где могут пригодиться эти данные. Да, они могут быть использованы в консоли. Но что, если нужно будет поменять формат вывода в консоль? Или вообще закинуть корни уравнения в форму с графическим интерфейсом? А может, отправить на сервер? Или записать в файл? Короче говоря, пишите гибкие и разбитые на задачи программы.
Представление данных
Данные хорошо бы предоставлять в удобном виде, чтобы их было легко распознавать и читать. Давайте напишем парочку методов, которые будут выдавать информацию об уравнении.
Например, его строковое представление. Прототип такого метода выглядит так:
|
1 2 3 4 5 6 |
/** * получить строку самого уравнения */ public String getEquationString() { return a + "*x^2+" + b + "*x+" + c; } |
Однако при таком подходе при отрицательных b или c строка будет иметь некрасивый вид. Например, при b=-3.5 и c=-17, получится такой результат: “2*x^2+-3.5*x+-17”. Этого хотелось бы избежать и не ставить плюс там, где число отрицательное. Для этого напишем метод, который будет заниматься этой задачей, и вызовем его из метода getEquationString():
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
/** * получить строку самого уравнения */ public String getEquationString() { return a + "*x^2" + getAddingValueStr(b) + "*x" + getAddingValueStr(c); } /** * получить строку прибавления заданного значения, * этот метод нужен, чтобы при прибавлении отрицательных чисел * в строке не получалось вот такого: "5+-7", а было "5-7" */ private String getAddingValueStr(double value) { String str = String.valueOf(value); String adding = (value >= 0) ? "+" : ""; return adding + str; } |
Теперь строка уравнения будет выглядеть как надо: “2*x^2-3.5*x-17”. Добавим ещё один, самый широкий по предоставляемой информации, метод getDescription(). Он будет включать в себя строку уравнения из getEquationString(), а также значение дискриминанта и найденные корни. Для формирования описания используем класс StringBuilder. Он позволяет более оптимизированно по затратам ресурсов складывать большое количество строк.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
/** * получить строку самого уравнения */ public String getEquationString() { return a + "*x^2" + getAddingValueStr(b) + "*x" + getAddingValueStr(c); } /** * получить строку прибавления заданного значения, * этот метод нужен, чтобы при прибавлении отрицательных чисел * в строке не получалось вот такого: "5+-7", а было "5-7" */ private String getAddingValueStr(double value) { String str = String.valueOf(value); String adding = (value >= 0) ? "+" : ""; return adding + str; } /** * текстовое (строковое) описание уравнения * с дискриминантом и корнями */ public String getDescription() { double discriminant = calcDiscriminant(); StringBuilder sb = new StringBuilder(getEquationString()); sb.append("\nДискриминант: ").append(discriminant); sb.append("\nКорни:"); double[] roots = findRoots(); for (double root : roots) { sb.append(" ").append(root); } return sb.toString(); } |
Для включения сообщения о том, что корней нет, когда размер массива roots равен 0, добавим проверку этого условия. Также среда разработки подчёркивает красным метод findRoots(). Это происходит, поскольку этот метод имеет в своей шапке throws QuadraticEquationException. То есть у нас два варианта. Первый: мы методу getDescription() такую же штуку впишем в шапку, и ловить это исключение придётся оттуда, откуда этот метод будет вызван. Второй: мы обработаем исключение QuadraticEquationException прямо внутри метода getDescription() в блоке try-catch.
Здесь я хочу поступить вторым образом. Если исключение возникнет, можно будет просто добавить его сообщение в формируемое описание уравнения. Таким образом, если корней бесконечно много, информация об этом будет записана.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
/** * получить строку самого уравнения */ public String getEquationString() { return a + "*x^2" + getAddingValueStr(b) + "*x" + getAddingValueStr(c); } /** * получить строку прибавления заданного значения, * этот метод нужен, чтобы при прибавлении отрицательных чисел * в строке не получалось вот такого: "5+-7", а было "5-7" */ private String getAddingValueStr(double value) { String str = String.valueOf(value); String adding = (value >= 0) ? "+" : ""; return adding + str; } /** * текстовое (строковое) описание уравнения * с дискриминантом и корнями */ public String getDescription() { double discriminant = calcDiscriminant(); StringBuilder sb = new StringBuilder(getEquationString()); sb.append("\nДискриминант: ").append(discriminant); sb.append("\nКорни:"); try { double[] roots = findRoots(); for (double root : roots) { sb.append(" ").append(root); } if (roots.length == 0) { sb.append(" нет корней"); } } catch (QuadraticEquationException ex) { sb.append(" ").append(ex.getMessage().toLowerCase()); } return sb.toString(); } |
Готово!
Итоговая программа
Вот написание кода класса “Квадратное уравнение” и подошло к концу. Протестируем его! Для тестирования класса QuadraticEquation напишем небольшой код в классе Main, чтобы запустить его.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import java.util.Scanner; public class Main { public static void main(String[] args) { System.out.println("Добро пожаловать в решение квадратных уравнений!"); Scanner scanner = new Scanner(System.in); System.out.print("Введите a -> "); double a = scanner.nextDouble(); System.out.print("Введите b -> "); double b = scanner.nextDouble(); System.out.print("Введите c -> "); double c = scanner.nextDouble(); QuadraticEquation equation = new QuadraticEquation(a, b, c); System.out.println(equation.getDescription()); } } |
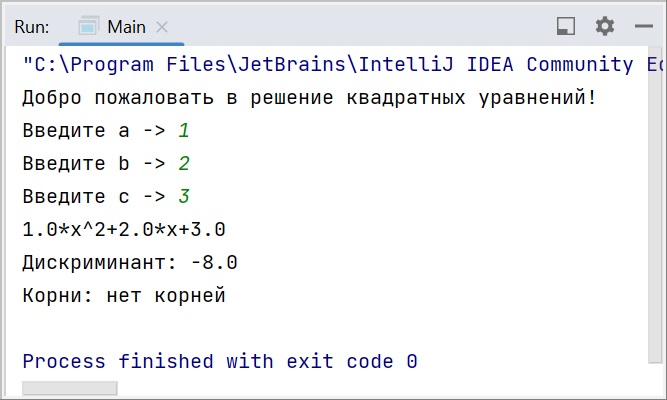
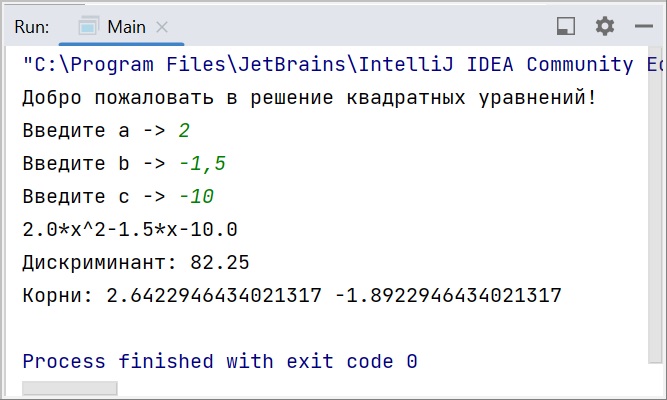
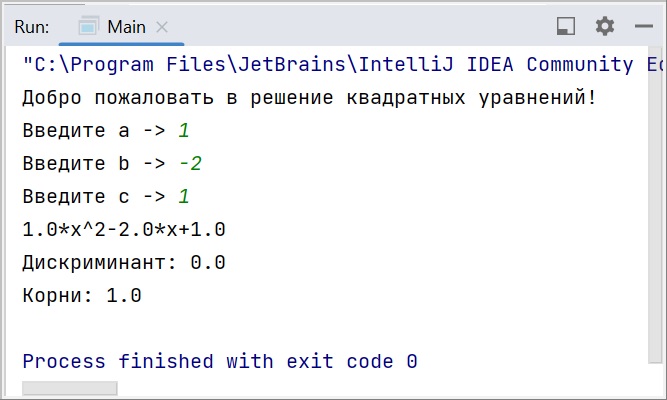
А теперь будем вписывать много разных вариантов значений коэффициентов. Это позволит увидеть, как наш класс справляется с различными жизненными ситуациями. Имейте в виду, что здесь не предусмотрена обработка ошибок при вводе double, если разделитель целой и дробной части не соответствует языковым настройкам вашего ПК. Так что при русской локализации разделять вводимые значения нужно запятой, а не точкой (например, “3,4” вместо “3.4”). Иначе возникнет исключение.
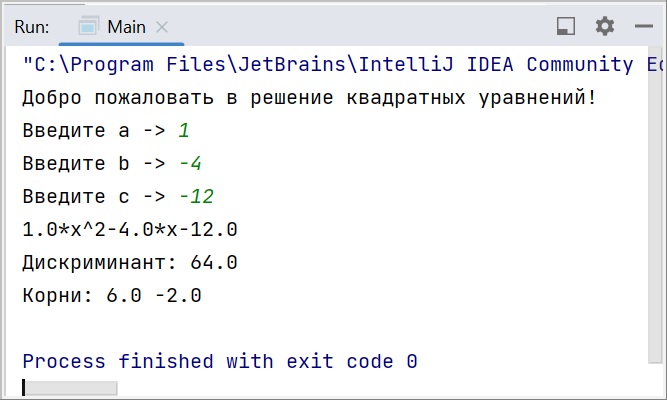
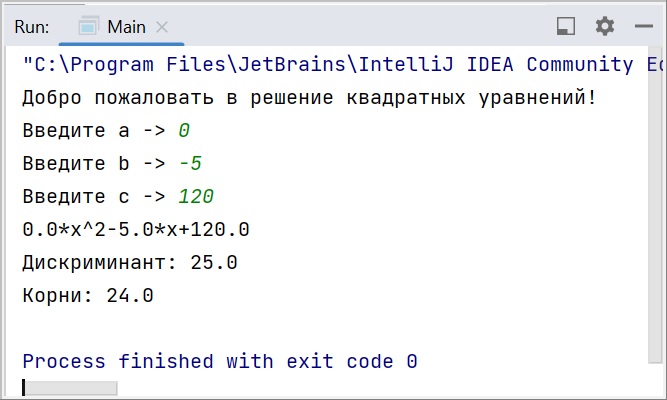
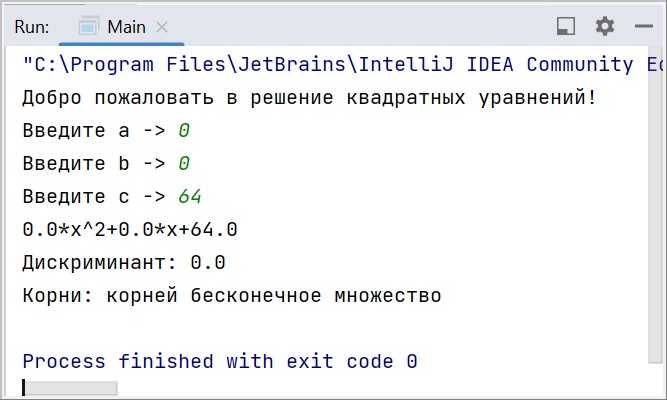
Полный код класса QuadraticEquation:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 |
/** * класс, представляющий собой квадратное уравнение * с коэффициентами a, b, c * * @version 1.0, 01.12.2023 */ public class QuadraticEquation { private double a; private double b; private double c; /** * конструктор с заданием всех коэффициентов сразу */ public QuadraticEquation(double a, double b, double c) { this.a = a; this.b = b; this.c = c; } /** * конструктор без аргументов * с начальными значениями коэффициентов - нулями, * чтобы коэффициенты можно было изменить позже */ public QuadraticEquation() { a = 0; b = 0; c = 0; } public double getA() { return a; } public void setA(double a) { this.a = a; } public double getB() { return b; } public void setB(double b) { this.b = b; } public double getC() { return c; } public void setC(double c) { this.c = c; } /** * нахождение всех корней квадратного уравнения, * причём их число может быть разным - от 0 до 2-х */ public double[] findRoots() throws QuadraticEquationException { if (a == 0) { return calcRootOfLinearEquation(); } double discriminant = calcDiscriminant(); if (discriminant < 0) { return getNoRoots(); } else if (discriminant == 0) { return calcOneRoot(); } else { return calcTwoRoots(discriminant); } } /** * получить отсутствие корней (0 корней), * пустой массив */ private double[] getNoRoots() { return new double[0]; } /** * рассчитать единственный корень * (когда дискриминант = 0) */ private double[] calcOneRoot() { double root = (-b) / (2 * a); double[] roots = { root }; return roots; } /** * рассчитать два корня уравнения * исходя из дискриминанта */ private double[] calcTwoRoots(double discriminant) { double rootOfDiscriminant = Math.sqrt(discriminant); double firstRoot = (-b + rootOfDiscriminant) / (2 * a); double secondRoot = (-b - rootOfDiscriminant) / (2 * a); double[] roots = { firstRoot, secondRoot }; return roots; } /** * рассчитать корень линейного уравнения, * то есть когда a = 0 и остаётся уравнение вида bx + c = 0, * которое легко решается переносом коэффициента c на правую часть с минусом * и делением его на коэффициент b */ private double[] calcRootOfLinearEquation() throws QuadraticEquationException { if (b == 0) { throw new QuadraticEquationException("Корней бесконечное множество"); } double root = -c / b; double[] roots = { root }; return roots; } /** * расчёт дискриминанта квадратного уравнения */ private double calcDiscriminant() { return Math.pow(b, 2) - 4 * a * c; } /** * получить строку самого уравнения */ public String getEquationString() { return a + "*x^2" + getAddingValueStr(b) + "*x" + getAddingValueStr(c); } /** * получить строку прибавления заданного значения, * этот метод нужен, чтобы при прибавлении отрицательных чисел * в строке не получалось вот такого: "5+-7", а было "5-7" */ private String getAddingValueStr(double value) { String str = String.valueOf(value); String adding = (value >= 0) ? "+" : ""; return adding + str; } /** * текстовое (строковое) описание уравнения * с дискриминантом и корнями */ public String getDescription() { double discriminant = calcDiscriminant(); StringBuilder sb = new StringBuilder(getEquationString()); sb.append("\nДискриминант: ").append(discriminant); sb.append("\nКорни:"); try { double[] roots = findRoots(); for (double root : roots) { sb.append(" ").append(root); } if (roots.length == 0) { sb.append(" нет корней"); } } catch (QuadraticEquationException ex) { sb.append(" ").append(ex.getMessage().toLowerCase()); } return sb.toString(); } } |
Пишите программы так, чтобы не стыдно было детям показать. А вообще, чем проще – тем лучше. Серьёзно. Громоздкий код никому не хочется разбирать. Со временем он начинает тухнуть.
В итоге, в этой статье мы написали прикольный пример ООП – создали класс QuadraticEquation для квадратного уравнения. Этот класс хранит в себе коэффициенты a, b, c, умеет находить свои корни и предоставлять описание уравнения.